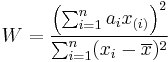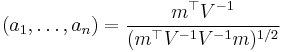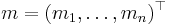Shapiro–Wilk test
In statistics, the Shapiro–Wilk test tests the null hypothesis that a sample x1, ..., xn came from a normally distributed population. It was published in 1965 by Samuel Shapiro and Martin Wilk.[1]
The test statistic is:
where
- x(i) (with parentheses enclosing the subscript index i) is the ith order statistic, i.e., the ith-smallest number in the sample;
- x = (x1 + ... + xn) / n is the sample mean;
- the constants ai are given by[2]
- where
- and m1, ..., mn are the expected values of the order statistics of independent and identically-distributed random variables sampled from the standard normal distribution, and V is the covariance matrix of those order statistics.
The user may reject the null hypothesis if W is too small.[3]
It can be interpreted via a Q-Q plot.
Contents |
Interpretation
Recalling that the null hypothesis is that the population is normally distributed, if the p-value is less than the chosen alpha level, then the null hypothesis is rejected (i.e. one concludes the data are not from a normally distributed population). If the p-value is greater than the chosen alpha level, then one does not reject the null hypothesis that the data came from a normally distributed population. E.g. for an alpha level of 0.05, a data set with a p-value of 0.32 does not result in rejection of the hypothesis that the data are from a normally distributed population.[1]
See also
- Anderson–Darling test
- Kolmogorov–Smirnov test
- Cramér–von Mises criterion
- Normal probability plot
- Q-Q plot
References
- ^ Shapiro, S. S.; Wilk, M. B. (1965). "An analysis of variance test for normality (complete samples)". Biometrika 52 (3-4): 591–611. doi:10.1093/biomet/52.3-4.591. JSTOR 2333709. MR205384.
- ^ op cit p. 593
- ^ op cit p. 605
External links
- Algorithm AS R94 (Shapiro Wilk) FORTRAN code
- Shapiro–Wilk Normality Test in R
- Shapiro–Wilk Normality Test in QtiPlot
- How do I interpret the Shapiro-Wilk test for normality?
- Online version of the Shapiro-Wilk test
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||